Genetic Algorithm Powerful Optimization Inspired by Nature

Introduction

Have you ever thought about how far we’ve come as humans and living beings? From the Stone Age to building computers and now nearing the creation of Artificial General Intelligence (AGI). Whether AGI is possible or not is a topic for another day. But it’s amazing to see what nature has given us. Natural selection improves the qualities of offspring, and humans keep getting smarter over time. We’ve come a long way, but nature is still incredible, constantly helping us evolve to become better versions of ourselves.

Who created this flow of nature? Why is everything like this? Who created us? Why does nature behave this way? No one really knows. In our busy world, people often forget the greatness of nature. Everyone is running, everyone is busy.

The Crypt Arithmetic Problem

During my 7th semester in my Artificial Intelligence course, I came across an interesting and famous problem in computer science: the Crypt Arithmetic Problem. Here’s what it means: Let’s say you have two words like SEND and MORE, and you add them to make MONEY. The task is to assign unique numbers to each letter so that when you add them up, they make sense arithmetically.

Example Problem:
SEND + MORE = MONEY
Solution found:

• D = 7, M = 1, N = 6, Y = 2, E = 5, S = 9, R = 8, O = 0

Solved equation:
9567 + 1085 = 10652

It sounds simple yet complex at the same time. As humans, we can solve these problems pretty well, but computers struggle. They need a way to represent the problem and then solve it. One way is brute force, where the computer tries all possible combinations until it gets the right answer. Today’s computers are fast enough to handle this quickly. Let me simplify this problem for you. There are some constraints that we need to follow in order to guess the numbers faster.

• The total number of distinct letters should be 10 or fewer.
• The length of the answer should not be shorter than the length of any operand.
• The length of the answer can be at most one more than the length of any operand.

Here’s how it looks:

  S E N D      9 5 6 7
+ M O R E    + 1 0 8 5
---------    ---------
  M O N E Y    1 0 6 5 2

tip

Hints for Finding Zeros and Nines:

• Columns like A+A=A and B+A=B indicate that A=0 (additive identity property of zero).
• In some cases, A can be 0 or 9, depending on whether there’s a carry-over of 1.

To find ones in additions:
Look at the left-hand digits. If single, they are probably 1. For example, in the puzzle SEND + MORE = MONEY, “M” can only equal 1 because it’s the carry from S+M=O (+10).

Genetic Algorithms

I was looking for an alternate way and found something called a genetic algorithm in my book. It made me stop and think. What’s a genetic algorithm?

Genetic Algorithm:
It’s an algorithm based on natural evolution. Just like nature evolves, the algorithm evolves to find the best solution.

Creating the Initial Population:
The first step in a genetic algorithm is to create a diverse initial population called chromosomes. This diversity increases the likelihood of finding the best solutions.

Assessing Individuals:
Each individual is evaluated based on their ability to solve the problem, usually by assigning a score called a fitness score. This helps identify the best performers who will contribute to improving the population.

Selection:
After evaluation, the best individuals are selected using methods like:

• Roulette Wheel: Individuals are selected based on their quality, with higher quality increasing their selection probability.
• Tournament Selection: Random pairs of individuals compete, and the best ones are selected.
• Elitism: The best individuals are directly chosen based on their quality.

Crossbreeding:
Pairs of selected individuals are combined to create new offspring. This crossbreeding enriches the population and helps evolve better solutions.

Mutation:
Random mutations introduce minor changes in individuals to maintain diversity and explore new solutions. These small modifications can lead to significant improvements.

New Generations:
The process is repeated over several generations, gradually improving the population until the optimal solution is found. This involves continuously creating, evaluating, selecting, crossbreeding, and mutating individuals.

Applications of Genetic Algorithms:

• Computer Science: AI, networking, and scheduling
• Robotics: Path planning and control
• Energy: Power distribution optimization
• Transportation: Traffic and route optimization
• Image Processing: Pattern recognition

Solving Crypt Arithmetic with Genetic Algorithms

To solve the Crypt Arithmetic problem using genetic algorithms, we define the fitness function as the absolute difference between the left-hand side (LHS) and the right-hand side (RHS) of the equation, aiming for a result of zero. Here is a high-level overview of the algorithm:

1. Initial Population: Create a diverse set of potential solutions.
2. Fitness Function: Calculate the absolute difference between LHS and RHS.
3. Selection: Choose the best individuals based on fitness scores.
4. Crossover: Combine pairs of selected individuals to create new solutions.
5. Mutation: Introduce random changes to some solutions for variability.
6. Iteration: Repeat the process for multiple generations until a solution with a fitness score of zero is found or a predetermined number of generations is reached.

I tested this approach and found that it works well in some cases but not in others, largely depending on the effectiveness of the selection and crossover steps.

Comparison

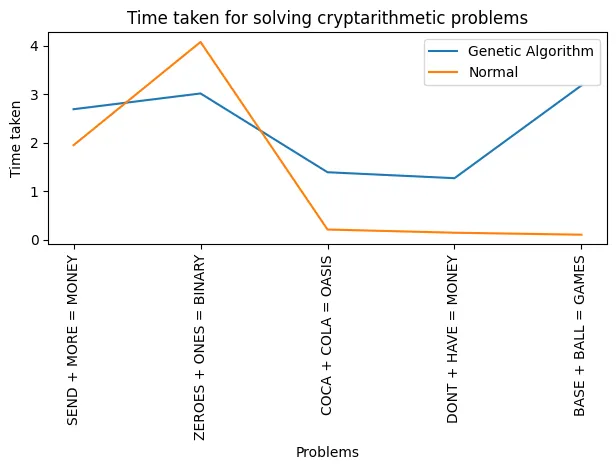
Nothing extraordinary, but we can see how awesome it looks. Overall, this graph suggests that the efficiency of each method varies depending on the specific cryptarithmetic problem being solved. The normal approach seems to perform exceptionally well on certain problems but poorly on others, while the genetic algorithm maintains a more consistent, moderate performance across all problems.

warning

[Note: The graph varies every time due to the generations of evolution and the population choices. It is just a simple implementation of a genetic algorithm with random parameters. Nothing fancy here, but I think after some optimizations in the algorithm, it can perform far better than the normal method.]

Look through this code: GitHub Repository

Conclusion

Nature’s evolution and the complexity of problems like Crypt Arithmetic show the amazing potential of both natural and artificial processes. As we keep advancing in technology, it’s important to remember the greatness of nature and the algorithms it inspires.

References

• The Knapsack Problem & Genetic Algorithms — Computerphile
• GitHub Repository